向量(vectors),是一个点指向另一个点的方向
AB=B−A
AB^=AB/∣∣AB∣∣
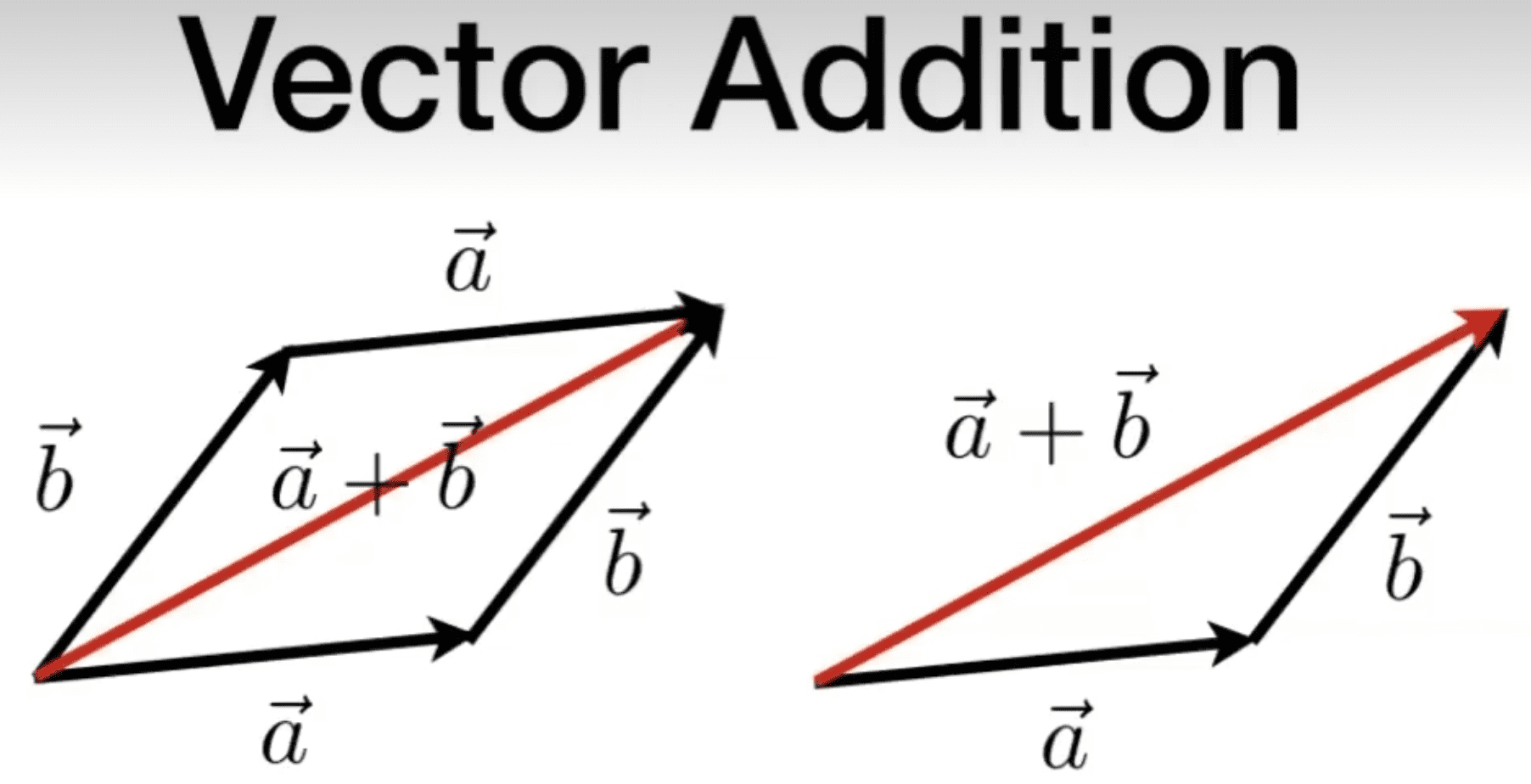 向量相加
向量相加a=(xy)aT=(xy)∣∣a∣∣=x2+y2
a.b=∣∣a∣∣∣∣b∣∣cosθ
这可以帮助我们快速的确定两个向量之间的夹角cosθ
cosθ=a^.b^
作用:
- 当点乘结果逐渐趋向1时,我们可以知道这两个向量的方向越接近
- 当点乘结果为0时,我们可以知道这两个向量的方向互相垂直
- 当点乘结果逐渐趋向-1时,我们可以知道这两个向量的方向相反
它满足运算的交换率,与结合率
a.b=b.aa.(b+c)=a.b+a.c
a×b=∣∣a×b∣∣=∣∣a∣∣∣∣b∣∣sinϕ
在三维坐标系中(右手坐标系中)
x×y=+z
叉乘没有交换率
a×b=−b×a
作用:
- 利用向量叉乘我们可以判断一个向量在另一个向量的左侧还是右侧
- 可以判断一个点在一个多边形点内侧还是外侧
必须满足(M×N)(N×P)=(M×P)
矩阵的乘积的结果中的单个目标等于矩阵A的行与矩阵B的列的元素分别相乘在并将元素相加
a1b1c1a2b2c2(A1B1A2B2)=a1×A1+a2×B1b1×A1+b2×B1c1×A1+c2×B1a1×A2+a2×B2b1×A2+b2×B2c1×A2+c2×B2
只有对角线为1,其他元素为0对矩阵为单位矩阵
I3×3=100010001
a.b=aTb=(xayaza)xbybzb=(xaxb+yzyb+zazb)
a×b=0za−yz−za0xzya−xa0xbybzb
SA=sx000sy000szxyz
SA=(1sxsy1)(xy)
Rθ=(cosθsinθ−sinθcosθ)
Rθ−=(cosθ−sinθsinθcosθ)
在平移变换中我们无法使用线性变换的法制进行转换
TA=(acbd)(xy)+(txty)
这时我们添加一个坐标 w 用来将它同化为线性变换
TA=100010txty1xyw=x+xtxy+ytyw2
当w=0时这是点坐标
P=(x/wy/w1)
当w=0时这是向量
V=(xy0)
x′y′z′w=adg0beh0cfi0txtytz1.xyzw
Scale
S(sx,sy,sz)=sx0000sy0000sz00001
Translation
T(tx,ty,tz)=100001000010txtytz1
Rotation
Rx(θ)=10000cosθsinθ00−sinθcosθ00001
Ry(θ)=cosθ0−sinθ00100sinθ0cosθ00001
Rz(θ)=cosθsinθ00−sinθcosθ0000100001
R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)N
其中
n=旋转的轴向量(过原点)α=旋转的角度
nT=n的转置N=0nz−ny−nz0nxny−nx0I=单位矩阵
